Basic Computations of esProc Sequences
Published on 05 September 14
Raqsoft0
A sequence is an ordered set consisting of some data, which are called members of the sequence. A sequence is similar to an array in high-level language, but the data type of its members not have to be the same. The following will explain its basic computation through creation, access, operators and functions.
Creation
1. Create with Constant
Bracketing members with “[]†represents sequence constant, e.g. 
A5=[15.2,"b",1] /Members of a sequence can be float, string and integer
B5=[A1:C3] /Members are cell area, i.e.
C5=[3,A5,B4] /A member of a sequence can also be a sequence,i.e.
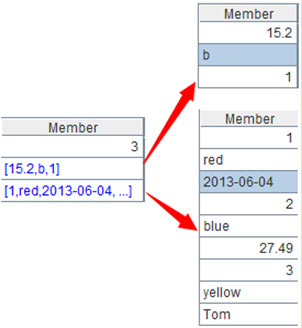
A6=[1,2,3,3] /Members can be repeated
B6=[] / A empty sequence
C6=[[]] /A non-empty sequence that its member is an empty sequence
Note: Members of a sequence can be any data types, including atom type, another sequences, records, etc. A sequence that all its members are integers is called an integer sequence.
2. Create with functions
to(2,6) / Numbers of the integer sequence are [2,3,4,5,6]. A integer sequence beginning with 1 can be expressed with to(6)
"1,a,b,c".array() /Split a character string into a sequence [1,a,b,c], a reversed joint can be expressed with [1,a,b,c].string()
periods@y("2012-08-10 12:00:00",now(),1) /Create a integer sequence for a period of time by dividing it into smaller time periods whose starting and ending points are in adjacent years, sequential value is ["2012-08-10 12:00:00","2013-01-01 00:00:00","2014-01-01 00:00:00","2014-07-01 10:10:41"]
file("e:/sales.txt").import@t() /Import records from structured text files to form a sequence, sequential value is:
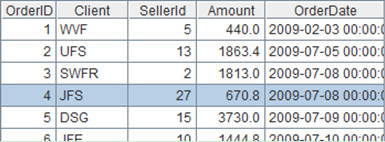
A sequence whose members are records is table sequence, which is often used to make computations of structured data. It’s not the focus in this article, for more information please refer to “Basic Computation of esProc Table Sequence and Record Sequenceâ€.
3. Create by computing
Description: read the text file sales.txt into table sequence A1, fetch column Client to create sequence A2; group the records according to Client to create sequence A3.
Code：
A1=file("e:/sales.txt").import@t()
A2=A1.(Client)
A3=A1.group(Client)
Note：
1. Value of sequence A2：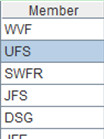 
2. Value of sequence A3：
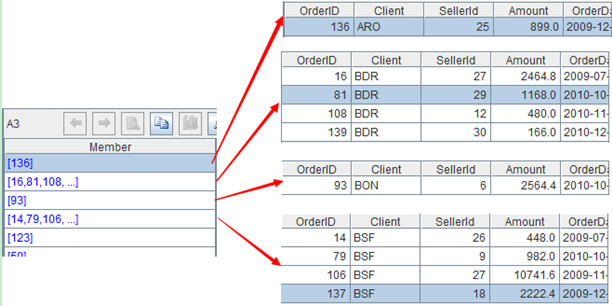
We can see that members of sequence A3 are a number of sequences whose members are records.
Accessing
4.Access members according to serial numbers
A1=[a,b,c,d,e,f,g] /Sequence A1
A1(2) /Fetch the second member whose value is string “bâ€, which equals to A1.m(2)
A1([2,3,4]) /Fetch members from the second to the fourth, whose value is expressed by the sequence [b,c,d]. Note that [2,3,4] is also a sequence(integer sequence). Intervals can be used to rewritten the expression as A1(to(2,4)).
A1.m(-1) /Fetch the last member. Note that m function must be used when fetching members backwards, the expression cannot be abbreviated to A1(-1).
5. Assignment and modification
A1(2)=r /Modify the second member to r, now value of sequence A1 is [a,r,c,d,e,f,g]
A1([2,4])=["r","s"] /Modify the second and the fourth member. A1=[a,r,c,s,d,e,f,g]
A1.Modify(2,["r","s"]) /Modify in turn from the second member, expression A1= [a,r,s,d,e,f,g] equals to A1([2,3])=["r","s"]
6. Add members
A1.Insert(0,"r") Add members at the end of the sequence, A1=[a,b,c,d,e,f,g,r]
A1.Insert(2,["r","s","t"]) /Insert three members consecutively before the second member, A1=[ a,r,s,t,b,c,d,e,f,g,r]
7. Delete members
A1.Delete(2) /Delete the second member
A1.Delete([2,4]) /Delete the second and the fourth member
Operators
8. Sets computation
Sets computation include ^ intersection, & union, \complement, and |concatenate, etc. For example:
A1=["a","b",1,2,3,4] /Sequence A1
B1= ["d","b",10,12,3,4] /Sequence A2
A1^B1 /Intersection, return the sequence made up of members of both thetwo sequences, value is ["a","b",3,4]
A1\B1 /Complement, a new sequence created by successively removing from A1 the members of B1, value is ["a",1,2]
A1&B1 /Union, value is["a","b",1,2,3,4,"d",10,12]
A1|B1 /Concatenate, value is ["a","b",1,2,3,4,"d","b",10,12,3,4]
Note: Both union and concatenate are created by combining members of two sequences in order. Common members only appear once in union while, in concatenate, all of them will appear.
9. Alignment arithmetic operation
Two sequences of the same length can make alignment operation according to members and return the sequence. The operation includes ++ (add), -- (subtract), ** (multiply), // (divide) and %% (complementation). For example:
A1=[1,2,3,4] /Sequence A1
B1= [10,12,3,4] /Sequence A2
A1++B1 /Counterpoint addition, value is [11,14,16,18]
10. Boolean operation
Two sequences can compare in alignment, the result is a Boolean type.
[1,2,3]==[1,2,3] /Comparative result is true
[1,B,3]<=[1,b,4] /Comparative result is true, because B is less than b
[1,2,3]<[1,3,4] /Result is true, because the second member of [1,2,3] is “2†, which is smaller than the second member “3†of [1,3,4]
Note: “in†function is used to judge the inclusion relation between sequences.
Functions
11. Aggregate function
Functions for sequences include sum, avg, max, variance,etc. For example:
A1=[2,4,6] /Sequence
A1.sum() /Summation, result is 12
A1.sum(~*~) /Quadratic sum, which equals to 2*2+4*4+6*6, result is 56. ~ represents each member of a sequence.
12. Loop function
Loop function can make computation aiming at every member of a sequence, and express complex loop statement with simple functions, including loop computation, filter, locate, look up, rank, sort, etc.
A1=[2,4,-6] /Construct sequence A1
A1=(~+1) /Add 1 to every member, result is [3,5,-5]
A1.select(~>1) /Filter out members that are greater than 1, result is [2,4]
A1.pselect@a(~>1) /Locate serial numbers of members that are greater than 1, result is [1,2]
A1.pos([-6,2]) /Look up serial numbers of members -6 and 2 in A1, result is [3,1]
A1.rank() /Rank of members of the sequence, result is [2,1,3]
A1.sort() /Sort in ascending order, result is [-6,2,4]; [2,4,-6].sort(~:-1) is the expression when sorting in descending order
This blog is listed under
Development & Implementations
and Data & Information Management
Community
Related Posts:
Post a Comment
